源码--HashMap计算真正容量的算法

java1.8 HashMap中根据入参初始值计算真正初始化容量的算法：
```java
  static final int tableSizeFor(int cap) {
      int n = cap - 1;
      n |= n >>> 1;
      n |= n >>> 2;
      n |= n >>> 4;
      n |= n >>> 8;
      n |= n >>> 16;
      return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
  }
```

### 举例推导
举例来看它的作用：
cap = 50，n = 49，二进制就是0011 0001
怎么计算n |= n >>> 1;呢？

这里需要先有一点预备知识：

无符号右移>>>：将二进制向右移动，低位消失，高位补0；

位或：将二进制每位上对应的数字进行或运算，1|1=1，1|0=1，0|0=0，有一个为1则结果为1。

那么计算过程就是：n的二进制是0011 0001，先将之无符号右移1位，变为 0001 1000；
再将原值0011 0001与右移后的数字进行位或运算，即
0011 0001 位或
0001 1000 等于：
0011 1001

然后计算   n |= n >>> 2;

...
计算完n |= n >>> 16;后，得到0011 1111
最后执行 (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
计算0011 1111 + 1 就变成了 0100 0000，就是2的6次方=64。

### 猜想->扩展
在进行了大量测试后我发现，此算法的计算过程是将cap-1的2进制中，从高位起第一个位上是1的位置开始，后面所有位置上的数全部变为1，这样任何一个数就变为0001111111这样的形式了；然后再加1，就变成了000100000，即2的n次方。

所以这个算法的目的就是将一个数n变成2的k次方；其中2的k次方是最接近且大于等于n的数（就是说k如果减一就会小于n，k如果加一就不会是最大于等于且接近n的了）。

那为什么右移的频率分别是1 2 4 8 16？为什么不是1 3 6 9呢？
答案是为了保证从第一个1位起，后面的每一位都是1，像车轮一样，从第一位，“碾”过每一位数字：
0010 0001 右移1位，位或得到：
0011 0001 将第一位1的后面一位变成了1。此时由于前两位都是1了，所以可以右移两位，利用前两位是1，进行位或，保证前两位1的后两位也是1，得到：
0011 1101 将前两位1后面的两位变成了1。此时由于前四位都是1了，所以可以右移四位，利用前四位是1，进行位或，保证前四位1的后四位也是1，得到：
0011 1111

为什么会有这样1的传播行为呢？因为是拿原值和向右移动后的值进行异或，异或的特点是只要有一个为1，则结果为1。假设原数最高位的1位置为k，向右移动之后的数的k-1位置上也是1，这样将原数与右移数进行异或，就会得到一个k位和k-1位置均为1的数；传播行为由此展开。下次位移时原数的k、k-1位置均为1，位移后k-2、k-3位置也均为1，这样将“此时的原数”和“此时的右移数”进行异或，就会得到一个k、k-1、k-2、k-3位置上都为1的新数字。...，经过这样紧密的1、2、4、8、16此位移，异或计算后，在不设限的前提下最终可以实现任意二进制位置均为1。

可以参考下面这幅图片：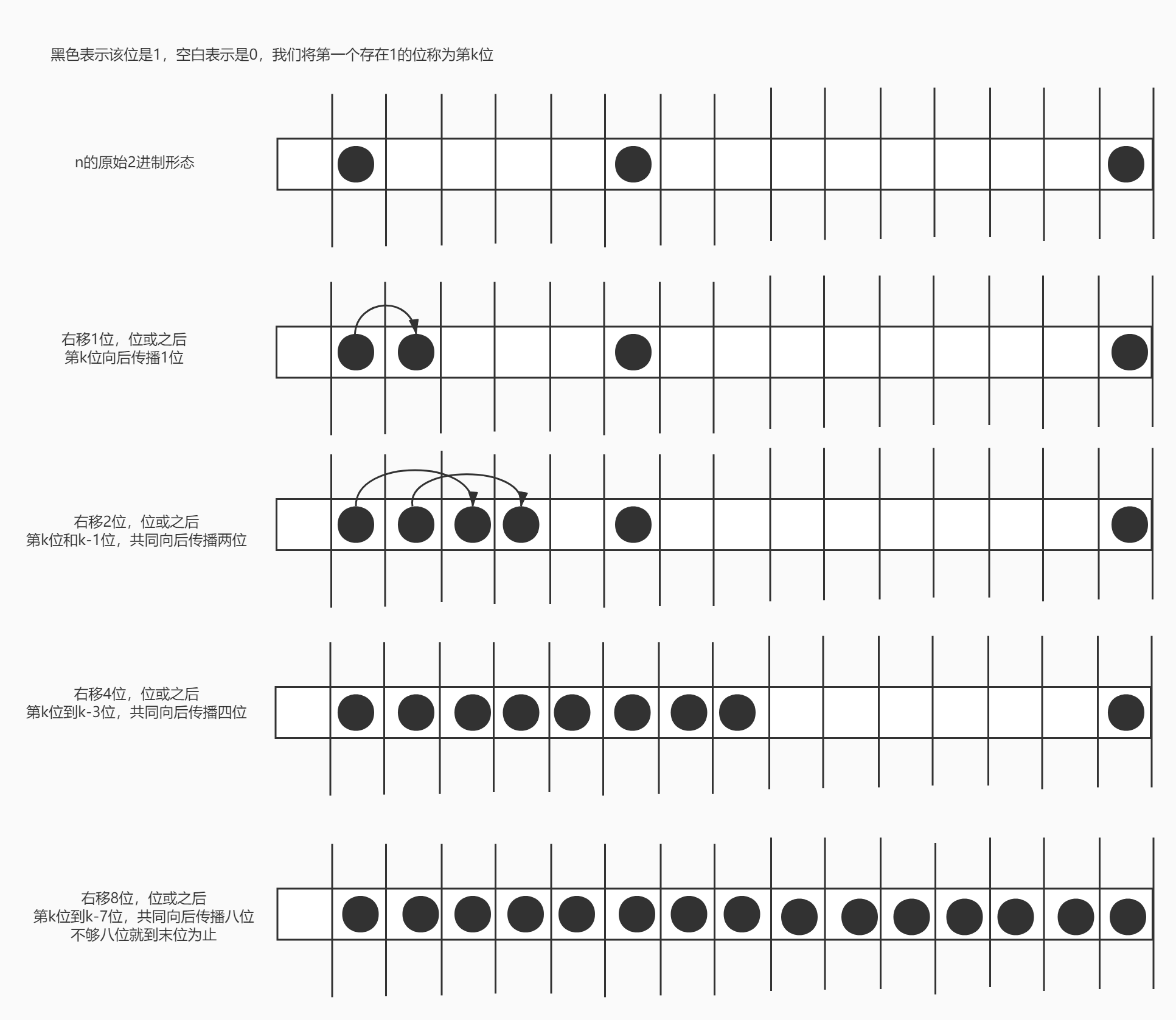

[![RQaVBV.png](https://z3.ax1x.com/2021/06/24/RQaVBV.png)](https://imgtu.com/i/RQaVBV)

### 循序渐进
这个数据有点小，我们换个稍微大点的：

00100000 00000000 00000000 00000000 右移1位，位或得到：
00110000 00000000 00000000 00000000 右移2位，位或得到：
00111100 00000000 00000000 00000000 右移4位，位或得到：
00111111 11000000 00000000 00000000 右移8位，位或得到：
00111111 11111111 11000000 00000000 右移16位，位或得到：
00111111 11111111 11111111 11111111 最后加1得到：
01000000 00000000 00000000 00000000 2的30次方：
1073741824
十亿七百多万

1 2 4 8 16这样的规律恰好保证不管你的数字是几，我都能一步挨一步从高位走向低位将每个位置均置为1。

1+1=2，2+2=4，4+4=8，8+8=16，16+16=32

那为什么到16就不再右移了？
因为已经达到了int最大值了，构造函数传入的参数是int类型的，16+16=32，对于32位的整型int来说足足够用。

### 悬崖勒马 -> 柳暗花明
不妨我们再大胆些，将入参数据换为：
01000000 00000000 00000000 00000000
经过
      n |= n >>> 1;
      n |= n >>> 2;
      n |= n >>> 4;
      n |= n >>> 8;
      n |= n >>> 16; 不断右移位或后
最终得到
01111111 11111111 11111111 11111111 最后加1得到：
10000000 00000000 00000000 00000000

咦，不对欸，java中int是4字节的，每个字节有8位，总共32位，但是最高位应该是符号位啊，正数的符号位就必须是0，1的话就是负数了啊。这就是函数第一行代码的高明之处了：int n = cap - 1;
先将入参减去1，这样如果我们的入参是01000000 00000000 00000000 00000000，那么减去1之后就变成了00111111 11111111 11111111 11111111，在二进制中直接降了一位。
接着再进行不断的右移位或，最后得到的是00111111 11111111 11111111 11111111，再加1之后变为01000000 00000000 00000000 00000000，这样就不会有负数的出现，而且将原始入参01000000 00000000 00000000 00000000进行函数运算后得到的还是01000000 00000000 00000000 00000000它本身，这很合理不是吗？入参本身就是2的n次方。

这个int n = cap - 1;解决了所有本身就是2的n次方的入参，可能会出现的错误：

如果没有int n = cap - 1;那么

0000 0010经过函数计算后得到的就是

0000 0100；

0000 1000经过函数计算后得到的就是

0001 0000；

0010 0000经过函数计算后得到的就是

0100 0000；

所有2的n次方经过函数计算后就变为了2的n+1次方，显然不符合HashMap取初始值的规则。

那么可能你会说，如果我的n是01000000 00000000 00000000 00000000，就是说cap是01000000 00000000 00000000 00000001，已经减一之后才是01000000 00000000 00000000 00000000呢？

这样是另一种情况，函数对他采取了另外的控制方法：

当cap是01000000 00000000 00000000 00000001，减一之后得到01000000 00000000 00000000 00000000

那么右移位或后结果是01111111 11111111 11111111 11111111，最后执行return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;时，就会触发(n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1; 最终返回了MAXIMUM_CAPACITY 。

实际上，只要当入参是int类型且大于01000000 00000000 00000000 00000000，即不管你是

01000000 00000000 00000000 00000001，或者

01000000 00000000 00000000 00010001，或者

01000000 00000000 00000000 00111000，再或者

01111111 11111111 11111111 11111111，经过右移位或之后的结果都是一样的，均为01111111 11111111 11111111 11111111（思考几步右移位或的终极目的），到最后都会触发(n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1; 最终返回皆为MAXIMUM_CAPACITY 。而MAXIMUM_CAPACITY 是int的最大值，却不是2的n次方，所以此函数在你传入的值大于2的30次方时，是无法返回给你一个通常情况下它会返回给你的结果的。（通常情况下它会返回给你一个大于等于入参且最接近2的k次方的值）这也很符合逻辑，因为当你的入参是大于2的30次方时，那么你需要的是2的31次方，可是函数没法返回给你2的31次方，因为入参和出参都是int类型的，int所能表示的最大值是2的31次方-1。

### 总结

int n = cap - 1;用来避免原本就是2的n次方的入参出现多余计算（或者说计算错误）。

n |= n >>> 1;
      n |= n >>> 2;
      n |= n >>> 4;
      n |= n >>> 8;
      n |= n >>> 16; 通过不断右移位或将自高位出现1的位置起，其后所有位置都置为1。

return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1; 用来避免大于01000000 00000000 00000000 00000000的入参最后得到负数10000000 00000000 00000000 00000000，对于大于01000000 00000000 00000000 00000000的入参，最后函数返回的总是MAXIMUM_CAPACITY。

综上，java1.8 HashMap中的tableSizeFor函数用来返回一个大于等于入参且最接近于2的k次方的数字，换句话说你的入参刚好小于等于2的n次方，那么它就会返回给你2的n次方；如果入参大于2的30次方，那么它总会返回给你MAXIMUM_CAPACITY ，也即2的31次方-1。

用此函数计算HashMap的实际容量，在大多数正常情况下总能得到一个大于等于人工分配容量值的2的n次方的数字。

源码--HashMap计算真正容量的算法

文章目录

发表评论